柏拉图与毕达哥拉斯派的关系值得引起重视，这不仅因为柏拉图与同时期的塔剌斯人阿尔曲塔斯（Ἀρχύτας）等一批毕达哥拉斯派学者过从甚密，还因为柏拉图的不同对话对数学的讨论在相当大程度上能够看到毕达哥拉斯派的痕迹。除我们熟知的《蒂迈欧》中毕达哥拉斯派对数字比例及宇宙几何学的讨论外（《蒂迈欧》35b-36b、53b-55c），在《美诺》中，苏格拉底还给出数个与数学对象相关的定义，他尤其侧重将图形看成“立体的边界或极限”（《美诺》76a）。这不仅与《理想国》中苏格拉底对平面几何、立体几何的划分形成对照（《理想国》7.526d-527c），还直接反映了阿尔曲塔斯的成果：阿尔曲塔斯本人在立体几何上造诣颇深，他通过构建两个比例中项（mean proportional）使立方体的体积翻倍，回应了名噪一时的“提洛问题”（Delian problem）。在《斐勒布》中，苏格拉底称“任何持存的事物都出自一和多，其自然本质也都由有限与无限组成”（《斐勒布》16c10-d2），并据此对辩证法展开论述。这里有限与无限的自然本质让我们联想到另一位毕达哥拉斯派学者菲洛拉欧斯（Φιλόλαος），他的宇宙同样诞生自有限与无限两项本原。

回到《理想国》，护卫者四“姊妹学科”的课程设置无疑受到毕达哥拉斯派影响。苏格拉底延续了阿尔曲塔斯的如下主张：

在我看来，学习数学的学生似乎有极好的知识……因为既然他们已经获得与整个宇宙的本质相关的知识，他们就能很好地把握每个事物的具体情况。他们向我们清楚传授了天体的速度及其升降方面的知识，还有几何、数字尤其音乐方面的知识。因为，这一类研究似乎是姊妹学科（ἀδελφεά）。（DK 47B.1）

于是，当苏格拉底（《理想国》7.531c）谈到毕达哥拉斯派和天文学家在做的事情时，我们有理由相信他对毕达哥拉斯派基于音程关系提出的数字比例了然于胸，且他此处考察的就是后者推理出的一些“和谐的”数字比例。这些“和谐的”数字比例不是数字两两随机组合，而是能体现出相互关联并且能被划为一类的基本属性或基本秩序。事实上，柏拉图心中的理想数字比例正是基于阿尔曲塔斯研究四度音阶（tetrachord）的音程划分时引入的概念。从和声学出发，阿尔曲塔斯将这点进一步明确，提出 ἐπιμόριος 即分超比（superparticular ratio）的比例类型，分超比在他看来是构成音乐和谐的基础。

分超比对柏拉图同时期的学者来说并不陌生。这是两个连续正整数之间的比值，其中较大的数比较小的数多出一个较小数的整数倍，可以表示为 (n +1 ) :n，具有 (n +1 ) /n =1 +1 /n 的关系。阿尔曲塔斯证明“分超比不能由某一比例中项（或几何中项）等分”（DK 47A.19）。包括欧几里得、托勒密在内的古代数学家普遍认为，相比于其他数学比例，如定超比（ἐπιμερής，写作 1 +m /n 或 r +m /n，r、m、n 均为正整数），分超比更加纯粹、简洁。C 一些分超比，如倍半比（ἡμιόλιος，意为包含 1 +1 /2）、倍三分之一比（ἐπίτριτος，意为包含 1 +1 /3），又与和声学中基于数学演绎推理得出的如纯五度、纯四度音程的比例数值相同。这种等同关系预示着，确定和声音阶中一些特定的、和谐的音阶关系，不仅可以通过经验实验，还可以通过对数学前提的演绎推理。

无论对以阿尔曲塔斯为代表的毕达哥拉斯派，还是对柏拉图，围绕数学前提的演绎推理都相当重要，因为他们由此可以从数学角度出发，在不参照任何可感物的情况下，对数与数之间的和谐关系给出说明：诸如分超比的数字满足某一比例结构的基本属性，这使其确实比其他数字更加和谐。反过来，此时天文学与和声学作为数学，其解释对象仍然是可感物，但不是在对可感物的属性作一项不确定的、可有可无的验证，而是在以数学方式证明，以此方式构造出来的可知对象具有某一共同属性，并且这种数学构造的结果前后一致，从而是有效的。

毕达哥拉斯派的数学在这一意义上仍不足以完整构成苏格拉底“真正的”数学，因为前者目前无法借助数学非假设的构造方式更准确地确定任一比例关系是否和谐。也就是说，如果毕达哥拉斯派无法证明每一个分超比都对应于一种和谐，他们就不可能把不同种类、不同程度的和谐准确分配到与其相称的比例中去，这使得他们不能说明和谐的数学关系将怎样与和谐本身一一对应。于是，柏拉图派可以就此提出不同意见，不同类别（γενή）的音阶与数学比例关系既然是从不同的对象或原则等一系列不同的起点演绎出来的，为何会在数学层面具有相关性？但这似乎不是毕达哥拉斯派关注的数学问题，因为这必然会将人从数学带往辩证法的领域。无论如何，这里能看到，毕达哥拉斯派认为，数字或数学对象可以反映可听见的和声的本质，而研究数字或数学对象的数学科目则是对解释和证明这一带有物理因果性的自然本质的方式的构想。现在的问题是，对柏拉图笔下的苏格拉底来说，他会希望数学家以同样方式教城邦护卫者数学吗？

我们看到，柏拉图在《美诺》《斐勒布》和《蒂迈欧》等对话中都沿用了毕达哥拉斯派的研究成果，他在《蒂迈欧》中更是将毕达哥拉斯派的数字比例同世界灵魂的构造联系起来。这使得我们相信，柏拉图认为毕达哥拉斯派的研究内容本身富有洞见，他的批评并不真正触及他们将世界数学化的过程本身，而只是局限在数学证成的方式上，且这不是一种戏剧对话式的反讽。例如，当我们问：毕达哥拉斯派推导出与和声音阶的划分相对应的数学比例，我们该如何验证其结论正确与否？对毕达哥拉斯派来说，他们的回应只能是回到琴弦长度的和声学实验，至多再附加吕克昂学园提出的要求，后者以更折衷的立场建议结合“数学式的和谐”，在感觉上辨别一段旋律是否和谐。但无论如何，毕达哥拉斯派无法切断可感物与数学比例间的关系：不管他们对数学的研究对象应满足的条件做出何种妥协，他们都不可能彻底放弃感官层面的诉求。

反过来，对苏格拉底来说，数学的研究对象一定不同于音乐，尤其不同于音乐在灵魂中创造出的“和声”，因为数学的目标已不再是证明一个和谐的音阶序列中一连串音符是和谐的，这是护卫者之前接受音乐教育时要完成的任务。如果苏格拉底“真正的”数学的研究对象能够达成某种统一，并且能够在不同事物中体现出一种普遍秩序，那么其结论就必定无法通过可感世界的感官经验来证明。感官经验如耳朵听到且产生知觉的对象，难免包含与数学演绎推理不相容的事实。这使得数学自始至终都无法依靠感官经验去验证其研究对象的统一性。为获得这种一致性，数学研究必须将感官经验排除在外，进而通过数学自身逻辑演绎的体系来维持和阐释这种统一性。苏格拉底数学的假设性前提的立场一旦成立，至少从两方面构成他对毕达哥拉斯派的批评。

其一，苏格拉底认为数学的研究对象不仅要与可感物相互分离，还跟我们听到的声音的本质全然不同，但毕达哥拉斯派却认为，数学的研究对象可以反映声音的本质，这构成了苏格拉底与毕达哥拉斯派的第一点分歧。对苏格拉底来说，数学就其自身而言构成一套系统，而声音以及由不同音高构成的和声音阶充其量不过是粗略地反映这套系统。他显然要求接受数学教育的学生在不借助感官、尤其在不借助耳朵听到和声的情况下，去说明和声学的研究对象，即与不同音高相关的数字，能够完全以其自身之故跟以经验方式划分音阶的比例关系相互分离，并且成为一个具有统一性的整体。

在《斐勒布》中，我们似乎能看到苏格拉底就这一方案展开的尝试。苏格拉底讨论音乐的“一”和“多”，尝试说明音乐的“一”及其本原（《斐勒布》16c5-18b），这可以理解成对和声学统一原则的一种探索。当然，从数学层面看，苏格拉底在《斐勒布》中的尝试确实可能引出本体论层面的一些问题：包括“和谐的数的关系”在内的数学研究对象，不同于辩证法研究的对象，后者研究数学的本原或诸如“一”这样的数字本身，这使得“和谐的数的关系”不可能是一类理式，而只能是理式的范例（παράδειγμα），或居于理式之下的不同的研究对象。可是苏格拉底没有明确，这些范例应理解成某类既不同于理式、又不同于可感物的居间实体，又或仅仅只是体现出不同理式之间的相互关系，从而不具有实体的性质。 但无论苏格拉底有没有这样尝试，毕达哥拉斯派都没有效仿苏格拉底，在数学层面寻求统一的本原，而正是这一本原将会作为城邦护卫者后续学习辩证法时的研究对象，使我们能够区分以数学对象为代表的思维对象与理式，并从思维和纯思（参见《理想国》7.535e）两个层面对数学和辩证法做不同研究。

其二，苏格拉底即使不反对毕达哥拉斯派的观点，也只会将“可听见的和声”看成以数学的基本属性为模板的产物，前者在以数学表示的基本属性上有缺陷、不完满，只有严格意义上基于数学的和声学才能超出实例化的数学命题，进而在可知世界层面构成某种统一的数学形式。苏格拉底并不排斥通过数学的方式研究可见世界中可以实例化的对象，这就好比算数学家用筹码表示数，平面几何学家画出一个几何图形，以此向学生“演示”几何图形的性质。A 但是，这些实例化的对象只是数学对象在可见世界中的表征，严格意义上对数学对象的演绎推理即“数学知识”将不会涉及这方面的内容。

针对和声学研究对象的本质，毕达哥拉斯派的观点却与之相反：数学或数字比例关系直接揭示了和声的本质与不同音高的关系，而正因为和声在音乐方面形成了一个有序的体系，才反过来说明作为和声本质的数学也是一个有序的体系。因此，苏格拉底与毕达哥拉斯派产生了第二点分歧：在数学研究中，苏格拉底根据前述统一本原演绎推理出数学研究对象的基本属性或基本秩序，这种对象的本质是数，反映数字本身的自然（φύσις），数学作为一个统一体系的原因仅仅在于其自身，是这个统一的事物的原因构成城邦护卫者所要学习的“数学知识”；毕达哥拉斯派则将数学对象的本质看成音乐和声，并且把数学演绎推理的结果解释成我们在“可听见的和声”中能够找到的、“可检验为真”（τὸ δοξάζειν ἀληθῆ）的信念，其统一性则是源自和声学作为一门经验科学所反映的经验事实，以及对这种经验事实做的演绎推理。

我们如果正确理解了苏格拉底对毕达哥拉斯派数学的批评，就将看到苏格拉底会对“什么样数的关系是和谐的”做出不同表述。苏格拉底不是效仿毕达哥拉斯派，将数的关系理解成与可听见的和声相对应的数字，而是将之理解成在可知世界中具有某一基本属性且能在类比意义上同“可听见的和声”作比较的数字。至少在《理想国》中，苏格拉底不接受作为音乐的和声学与作为数学的和声学二者有更紧密的联系，前者至多在心理层面对后者起到暗示作用，且这种暗示似乎表明我们无法从可见世界中获得某种为“真”的知识或信念。不过，柏拉图在《理想国》中也没有借苏格拉底之口明确说明音乐和数学层面两种不同的和声学之于灵魂具有何种形式因果性，这是他在《蒂迈欧》中完成的任务：如果不能通过数学方法得出关于可感物的某种为真的信念，那么就无法确定，根据可感物的经验进一步推理的数学研究对象，其作为一门知识可知且可靠的依据来自哪里，因为这种知识的可知性只可能源自可感物的“理式”所依据的向上的实在和真理是否可知、是否可靠。

亚里士多德在《形而上学》中首先认定毕达哥拉斯派最早从事数学研究，他们“不仅推进了这方面的研究，而且也在这种研究中受到培育”（1.985b24-25）。紧接着，亚里士多德开始讨论柏拉图哲学，他对柏拉图数学研究的对象总结如下：

再有，在可感对象与理式之外，他（柏拉图）说还有数学对象，处于中间位置。它以其永恒不变区别于可感对象，区别于理式之处则在于有许多相似，而理式本身则在任何情况下都是唯一。（1.987b14-18）

基于这两段文本的关联性，可以认为亚里士多德将毕达哥拉斯派的数学研究看作数学哲学的起点；相应地，在《理想国》中，为使灵魂从可见世界转向可知世界，苏格拉底尝试建立新的数学标准，以此同毕达哥拉斯派竞争。这意味着，《理想国》中苏格拉底“真正的”数学与亚里士多德《形而上学》中讨论的柏拉图的数学哲学有相同的出发点。如果这一比较成立，则亚里士多德列举的柏拉图数学对象的特征就是苏格拉底“真正”数学的特征：一，数学研究的对象是永恒的；二，数学对象缺乏运动，是不变的；三，在基于同一理式的情况下，数学对象可以有众多（甚至无限）B 的实例；四，数学对象彼此相似，但只有理式是“一”。

“真正的”数学首先区分了可感对象与理式的不同特征。首先，可感物是杂多、短暂的，而理式则与之相反。其次，理式是其自身的例证，而可感对象只在某种限定条件下是理式。例如，在《斐多》中，苏格拉底称“一根木头等同于另一根木头”，这只是比较意义上的“等同”，并非“是”本身（《斐多》74a）。在这方面，数学对象与可感物一样：两个篮子和两个苹果，各自构成“二”这个数，但这里的“二”只是以不同的方式在记数，只能看成“两个杂多”，而不是“数字二”或绝对的“二”的理式。同样，如图所示，在几何学中，三角形 ABC 等于三角形 ADC，但两个三角形不是绝对等同，最多不过“趋近完美”地呈现出三角形本身的理式。单就数学对象来说，苏格拉底的这一区分让人疑惑：如果我们按照前述苏格拉底对毕达哥拉斯派的第二点批评，认为数学对象的演绎推理将不会涉及我们这里列举的三角形 ABC、ADC 或平行四边形 ABCD 这类可实例化的对象，那么，当我们在研究数学对象时讨论诸如平行四边形、三角形、对角线等概念，我们能够从中知道些什么？或者说，苏格拉底“真正的”数学研究的对象到底是什么？

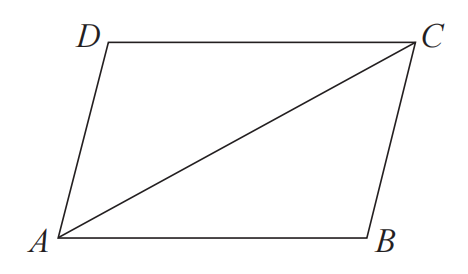
亚里士多德对苏格拉底“真正的”数学的核心观点是，数学研究的对象必须是充分的，是建立在理性认知方式之上的知识，并且是基于数学定理构建的统一体。数学定理讨论平行四边形 ABCD、对角线 AC 以及两个相等的三角形 ABC 和 ADC，但这些可感对象要成为知识的对象，就必须严格按照定理的规定存在。例如，任何平行四边形都能被一条对角线平分，为知道这点，我们首先要有平行四边形的知识，而后才能对平行四边形对角线的性质产生认识，这里已知的平行四边形 ABCD 则只是平行四边形本身的精确示例。此外，数学研究的对象不能是平行四边形本身，因为后者会分成两个三角形本身，但理式本身却不可分，这意味着数学研究的对象不是理式本身。

学界将这一观点称为“主体中心观”（subject centric view）。当苏格拉底在《蒂迈欧》中分别谈到三角形和正多面体是平面几何和立体几何的基本要素，他显然参照了“主体中心观”。因为正多面体由三角形构成，而理式不由其他对象构成，也不能构成其他对象，所以正多面体和三角形都不是理式；但因为二者将分配给火、土、水、气四元素（《蒂迈欧》55d9-56c1），四元素又是构成宇宙的基础，二者就成了数学天文学研究的对象，是天文定理的充分主体。这意味着，三角形和正多面体因其短暂性，必定只能成为数学研究对象不完美的例证。质言之，一个人如果接受“主体中心观”，并且承认可感物作为数学研究的对象不充分，他就只能将亚里士多德称作“处在中间位置的数学对象”看成一类居间实体，而非看成反映居于可感物与理式之间的某种关系。

“主体中心观”包含这样一个前提：以平行四边形为例，一个平行四边形及其对角线的构造必须真实存在于某处，才可以成为数学研究的主题。这回应了苏格拉底为何会在接受毕达哥拉斯派的基础上批评后者的数学研究：一方面，数学研究不只依赖于演绎推理，而且必须指向可感物、某个实际存在的事物，以确保其符合相关数学定理的命题；另一方面，根据特征一和二，数学研究的对象本身又必须超越这些有缺陷的、不完满的可感物。因而，苏格拉底在数学研究对象与可感物相互分离的基础上提出一种新的可能：数学研究对象类似可感物，必须是实例化的科学命题，但同时作为知识的对象又必须同理式一样永恒不变。相应地，与数学研究对象相关的定理不是一个假言命题。因为，在推理一个平行四边形时，必须存在某个区别于平行四边形理式的实际存在的平行四边形，且我们是在对这个实际存在的平行四边形而非其理念做推理。同样，通过演绎推理掌握关于平行四边形的定理时，这里的数学定理不能基于一个未经证实的假设，正如苏格拉底所说，假设必须在辩证法中得到证实。

亚里士多德在处理数学居间对象的问题时（《形而上学》3.997b35-998a19），给出一则与天文学有关的论证，以支持其“主体中心观”。几何学家认为，圆只会在一个点上同直线接触，但普罗塔戈拉指出这不可能，因为真实的圆箍与直杆不可能只在一点上接触。于是，亚里士多德给出推论，行星真实的运动轨迹不是如天文学家计算的那样满足科学的要求，相应地，几何学上的点也不具有与实际群星同样的本性，这意味着可感物不具备数学研究对象要求的属性精确性（3.997b34-998a6）。稍后，亚里士多德称，支持数学居间对象的人认为数既是存在、实体，又与可感世界相互分离，数学定理不适用于可感物，但关于数学定理的陈述必须为真（14.1090a35-b5）。显然，亚里士多德将数学居间对象主体中心的观点归于柏拉图派。基于此，这里沿用亚里士多德的观点，得出数学对象的第五特征：具有属性精确性。这意味着不只存在可供数学研究的对象，这些对象还必须具备数学演绎推理时包含的属性，这些属性通过相关的数学定理得到充分表达，而可感世界中的其他对象因为与数学研究对象不同便无法拥有这类属性精确性。

以平行四边形 ABCD 为例，能够开展数学研究的对象是点 A、点 B 和线段 AB 等点和线，而数学演绎推理包含的属性则是平面几何基于点线面公理建立起的对线段及图形长度、角度、位置关系等的讨论。说“平行四边形是数学研究的对象”时，必须同时满足上述两则条件，以具备数学研究对象具有的属性精确性。

需要指出，虽然亚里士多德在《形而上学》卷一讨论柏拉图数学研究对象时没有列出特征五，但这不意味着特征五与特征一至四是割裂的。如果说特征一、二讨论所有知识的一般属性，特征三、四强调若干相似的数学对象分有一个共同的理式，特征五便是在数学对象作为知识对象的基础上，更具体地规定其需要满足哪些条件，以体现其作为一门科学知识的属性。这使得数学对象不仅可理解，而且能够严格按照数学演绎推理的形式因果关系加以明确。

尽管如此，我们很难从《理想国》中苏格拉底批评毕达哥拉斯派数学研究的内容中找到证据，完整建立起数学知识与引出数学演绎推理的纯思之间的关系。因为，正如前文谈到的，毕达哥拉斯派对因果性的理解基于诸如音乐等研究对象物理性的自然本质，其因果关系的出发点是物理因果性，而苏格拉底“真正的”数学实际上已经表明，数学的因果性不是物理的因果性。事实上，苏格拉底用“实在”或“存在”而非用“理式”来表示可知世界中思维的确定性，同可见世界中与“意见”相关的“生成”或“生成物”相左。尽管“实在”始终是数学研究的目的（7.523a3、7.524e1、7.525b5、7.525c5-6、7.526e6-7），但苏格拉底没有真正处理数学实在与理式实在的不同之处，这意味着我们不仅无法仿照线段喻确定数学对象是如理式一样独立于可感物之外，或是存在于可感物当中，也无法根据理式、可感物和中介数学对象三分的本体论，明确知道数学对象如何基于辩证法形式因果的假设得到说明。

为什么苏格拉底在《理想国》中回避深入探究居间数学对象的本体实在论问题？我们可以选择相信，这是他有意为之，就像他早前在谈到知识时避免谈到“善”的问题（6.506d-e，参见 6.509c、7.517b-c），在谈到数学时避免谈到辩证法（7.533a）。他建立“真正”数学的目的是批评毕达哥拉斯派的数学“不完整”，“没有达到任何事物的目的”。当他通过具体规定数学研究对象成功达到这一目的时，他没有继续就这一问题推进下去，而是以引发疑问的方式留白，意在邀请城邦护卫者、邀请作为读者的我们，通过学习“真正的”数学去填补这一空白。

柏拉图无疑在《理想国》关于数学教育的讨论中吸纳了大量毕达哥拉斯派的元素，这不仅体现在他采纳了后者四“姊妹学科”的数学课程设置，还体现在他借助阿尔曲塔斯的数学比例研究，将包括天文与和声学在内基于经验推理的科目纳入城邦护卫者的教育。我们并不期待从苏格拉底与格劳孔的对话中看到对任何实质性数学问题的分析，或对这门学科的课程内容做更细致的描绘，因为苏格拉底实际上区分了教育护卫者的数学与具有现实用途的数学：后者的目标是买卖算账、行军打仗时的排兵布阵等，而不是把学生的灵魂从生成领域领向更高的实在和真理的领域，为城邦统治者后续的辩证法训练做准备。

一些讨论通常会将毕达哥拉斯派的和声学与天文学研究看成与具有现实用途的数学是一回事，认为柏拉图的批评仅仅在于他们利用数学来观测天体和给乐器调律。但这没有真正涉及柏拉图笔下的苏格拉底批评毕达哥拉斯派的核心。毕达哥拉斯派同苏格拉底一样，都能从数学演绎推理出发，在不参照任何可感物的情况下，对天文与和声学中数与数之间的关系做出回应，毕达哥拉斯派的数学研究不应当简单地被看成对确定“技术”的追求。

通过分析《理想国》文本可以看出，既然毕达哥拉斯派选择把数学演绎推理的结果解释成与“可听见的和声”相关的信念，他们要么不寻求这些结果经过辩证法形式因果的验证，要么仅仅回到数学演绎的经验起点、回到和声学实验来验证其结果是否为真，这便与苏格拉底“真正的”数学“本性引领纯思”的要求产生冲突。于是，苏格拉底对毕达哥拉斯派的数学提出了两点批评：它最终选择回到研究对象的经验起点，而非进一步上升到辩证法对本原的讨论，并且其数学研究对象的本质不是数学，而是可感对象。这两点在他看来都误解了“真正的”数学内容。比较亚里士多德《形而上学》，可以归纳出《理想国》中苏格拉底“真正的”数学应具有的五项特征：首先，数学研究的对象是永恒的；其二，这一对象是不变的；其三，它可以有众多实例；第四，不同的数学研究对象彼此相似，但只有理式是“一”；最后，数学研究的对象必须具有与科学相关的属性精确性。建立在这五项特征基础上的“真正的”数学，不仅对哲学辩证法的探究有必要且有益，还能将学习数学的城邦护卫者以及学习数学的我们直接引向理式本身，“使灵魂到达实在”。

作者简介

薛璟明，四川成都人，中山大学博雅学院，主要研究方向为古希腊哲学、古代自然科学史。

 钟碧莉｜彼特拉克的月桂树与毕达哥拉斯的字母

 新刊｜周小龙：理智在混合生活中的作用——评多萝西娅·弗雷德的《斐勒布》译疏

 思考亚里士多德笔下的苏格拉底

 经典与解释·壹卷 | 《柏拉图的数学哲学》（刘溪韵译 梁中和校）

 新书上市丨施特劳斯《苏格拉底面对美诺——柏拉图〈美诺〉讲疏（1966）》（陈明珠 译）

 新刊发布｜《古典学研究》2025年秋季号

编辑｜安雪怡　王涵宇 

欢迎关注

插图来自网络，与文章作者无关。

如有涉及版权问题，敬请联系本公众号删除。